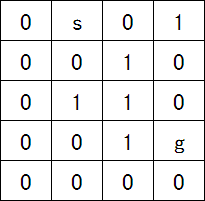
1.课题

给定一个列数为M，行数为N的方格棋盘。
棋盘上定义起点、终点、道路、墙壁。
棋盘上必有一个起点和一个终点，剩余方格必定为道路或者墙壁。
现寻求角色从起点到终点的最短路径长度，其中角色只能上下左右移动。

2.输入与输出

棋盘信息由文本文件提供。
第一行为列数M与行数N，由空格隔开。
第二行以后的N行，各为由空格隔开的M个字符。
其中，“s”代表起点，“g”代表终点，“0”代表道路，“1”代表墙壁。

棋盘示意图

通过标准输出，给出从起点到终点的最短长度。
如果不存在路径，则输出“Fail”。

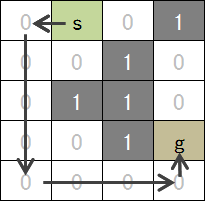
某一种最短路径

3.基本思路

采用广度优先搜索思路（BFS），从起点出发，计算起点到周围方格的举例，不断扩散范围直至找到终点。
定义一个队列，用于存储即将测量其最短路线长度的方格，然后把起点放入队列，并且初始化步数为1。
然后循环下列操作：

从队列中取出一个方格
该方格上下左右四个方格如果不是墙壁，加入队列
如果上下左右四个方格为终点，则直接输出步数作为结果，结束程序
步数加1

直至队列为空。
如果队列为空导致循环结束，则意味着没有路线能连接起点与终点，输出“Fail”。

4.Python实现

import collections

f = open("data.txt", "r")

input_line = f.readline()
input_line = input_line.strip('\n')

matrix_info = input_line.split(" ")
w = int(matrix_info[0])
h = int(matrix_info[1])

dirs = [(-1, 0), (0, 1), (1, 0), (0, -1)]

matrix = []

start_x = 0
start_y = 0

goal_x = 0
goal_y = 0

for i in range(0, h):
    input_line = f.readline()
    input_line = input_line.strip('\n')
    row = input_line.split(" ")
    for j in range(0, w):
        if row[j] == 's':
            start_x = j
            start_y = i
    matrix.append(row)

q = collections.deque()
q.append((start_x, start_y))
visited = set()
visited.add((start_x, start_y))

step = 1
flag = False

while q:
    for _ in range(len(q)):
        x, y = q.popleft()
        for dx, dy in dirs:
            nx, ny = x + dx, y + dy
            if 0 <= nx < w and 0 <= ny < h and matrix[ny][nx] != '1' and (nx, ny) not in visited:
                visited.add((nx, ny))
                q.append((nx, ny))
                if matrix[ny][nx] == 'g':
                    print(step, end='')
                    flag = True
                    break
        if flag:
            break
    if flag:
        break
    step += 1

if not flag:
    print('Fail', end='')

5.思考过程

最开始拿到这个问题的时候，直观想法是将棋盘抽象为无向图，每一个方格都看作是一个点，可以通行的点（起点、终点、道路）之间具有一条长度为1的边。
然后采用迪杰斯特拉算法求起点到终点的最短路径长度，采用Java实现。
但是在大规模数据上（大小为1000*1000的棋盘上）出现了Runtime Error。
因为是黑盒测试，所以不知道具体数据和错误信息。
因为其他普通数据（100*100以下的棋盘）没有问题，所以很难认为是数组越界等实现上的问题，可能还是数据规模过大导致的内存泄漏的原因。

于是更改思路，尝试了Python实现的A*算法，但是可能与其复杂的数据结构有关，大规模数据上出现了超时（16秒）的问题。
最后尝试了广度优先搜索，大规模数据在1.5秒以内运行完毕，成功通过所有测试数据。

6.相关问题

在调查的过程中，发现LeetCode上有一道十分类似的问题：1091. Shortest Path in Binary Matrix。
只不过这道问题里，角色还可以斜着移动，共有八个移动方向。
解决这个问题，只需要把向量集合改成八个方向就可以了。

// 上下左右四个方向
dirs = [(-1, 0), (0, 1), (1, 0), (0, -1)]

// 上下左右+对角线八个方向
dirs = [(-1, -1), (-1, 0), (-1, 1), (0, 1), (1, 1), (1, 0), (1, -1), (0, -1)]

7.测试数据

最后附上随机测试数据生成器：generator.py。

Reference Source:

1091. Shortest Path in Binary Matrix (Python)

广度优先搜索解决方格棋盘最短路径长度问题

Contents