1.动机

代码复用的概念自然不必赘述，因为本身就是十分自然的行为。把写过的代码复制粘贴过来，或者直接到网上抄，都算是代码复用。
代码复用的最终目的是为了减少重复劳动，提升效率，毕竟不需要重新敲同样的代码了。
不过上面这些属于体力劳动，好的代码复用还能减少重复的脑力劳动，让思路更清晰，把精力放在更需要创造性的地方。
说出来是很简单直白的道理，面向对象编程的概念也是老生常谈了。但是实际开发中好像确实没怎么有意识地思考过这个问题。
这次就通过自己整理的线性代数JS库，实践了一次JavaScript的代码复用过程。

2.哪些代码该拿来复用？

考虑二维坐标系中两条线段交点的问题。
这个问题有两个要素：

如何得到线段
如何求相交问题

第一个问题，线段可以由两个端点确定。
所以对于线段，可以用下列类的伪代码表示：

class Ray{
  number x1,
  number y1,
  number x2,
  number y2
}

由于一个线段有两个端点，二维坐标系中一个点需要用两个数字表示其坐标，所以线段类需要维护4个成员变量（properties）。

但是其实其中x1和y1描述的是同一个端点，其两者之间的关系要比与剩下两个的要更紧密。
所以可以进一步整合成员变量，将关系相近的变量两两整合成新的类，这里用向量表示。

class Vector{
  number x,
  number y
}

class Ray{
  Vector v1,
  Vector v2
}

如此一来就得到了两个类：线段类与向量类。
线段类中的成员变量缩减成了两个端点的位置向量了。

不过，上面只思考了端点这一个重要属性。对于线段而言，还有一个重要属性，那就是长度。
如果用Ray类来求线段长度的话，方法是求两个端点的位置向量的差的模，涉及到幂与方根的运算。

线段的长度这个很基本的属性，每次都需要这样运算的话，显然程序整体的运行过程不够精简。

另外，对于两个平行线段而言，平行这一重要特征，也没有办法在端点的位置向量上直观体现出来，只能去运算模与端点单侧坐标差值的比值才能确定是否平行。

也就是说，这个线段类的成员变量应该重新考虑。

如果知道线段的一个端点的话，可以大体知道线段的位置，但是还有不知道的信息：

线段的长度
从端点出发延伸的角度，即线段的角度

将这两个信息整合起来形成一个新的成员变量的话，就是线段的方向变量。

重新设计线段类：

class Vector{
  number x,
  number y
}

class Ray{
  Vector pos,
  Vector way
}

用线段其中一个端点的位置变量pos来确定线段的位置，用线段的方向变量way来表示线段的方向。

这样，只需要计算way的模就可以确认线段的长度，比较两个线段是否平行也只需要比较way就可以了。

但是还是会有不少想要获取线段端点位置的时候，线段端点位置直观上也算是线段的某一个属性。
但是线段的另一个端点的位置变量其实是可以通过pos和way计算出来的，如果再把它塞进到成员变量的话就会造成冗余和双主值的问题。

这个时候最好的做法是用存取器（accessors）来表示这种可以用成员变量派生出来的属性。
存取器分为赋值器（setter）与取值器（getter），线段的端点通常是固定的，所以只使用取值器来表示。

在线段类内添加端点位置的存取器：

class Vector{
  number x,
  number y
}

class Ray{
  Vector pos,
  Vector way

  get begin(){}
  get end(){}
}

这样就可以用调用成员变量的方式（ray.begin）的方式来获取派生出来的属性了。

第一个问题解决了，下面是第二个问题：如何求相交问题。

在考虑线段相交之前，可以先考虑直线相交。

比如求以下两条直线（ $t_{1} \neq t_{2} \wedge t_{1}, t_{2} \in R$ ）的交点：

$y-y_{1}=t_{1}\left(x-x_{1}\right)$
$y-y_{2}=t_{2}\left(x-x_{2}\right)$

很简单的数学问题，交点 $\left (x, y\right )$ 的坐标值分别如下：

x=\frac{t_{1} x_{1}-t_{2} x_{2}-y_{1}+y_{2}}{t_{1}-t_{2}}

y=t_{1}\left(x-x_{1}\right)+y_{1}

把上述算式映射到Ray类可以发现， $t_{1}$ 和 $t_{2}$ 分别就是方向向量y坐标与x坐标的比值，而定点 $\left (x_{1}, y_{1}\right )$ 和 $\left (x_{2}, y_{2}\right )$ 可以用端点的位置向量表示。这样就可以根据上述算式计算出交点的坐标。

但是上述计算是在直线的前提之下，只要不平行必有交点，但是线段未必。通过上述算式计算出来的交点只是两条线段所在直线的交点，还需要计算交点是否同时位于两条线段上。

如下图所示，线段f和线段g所在直线h和i的交点为P，但是线段f和线段g不相交。

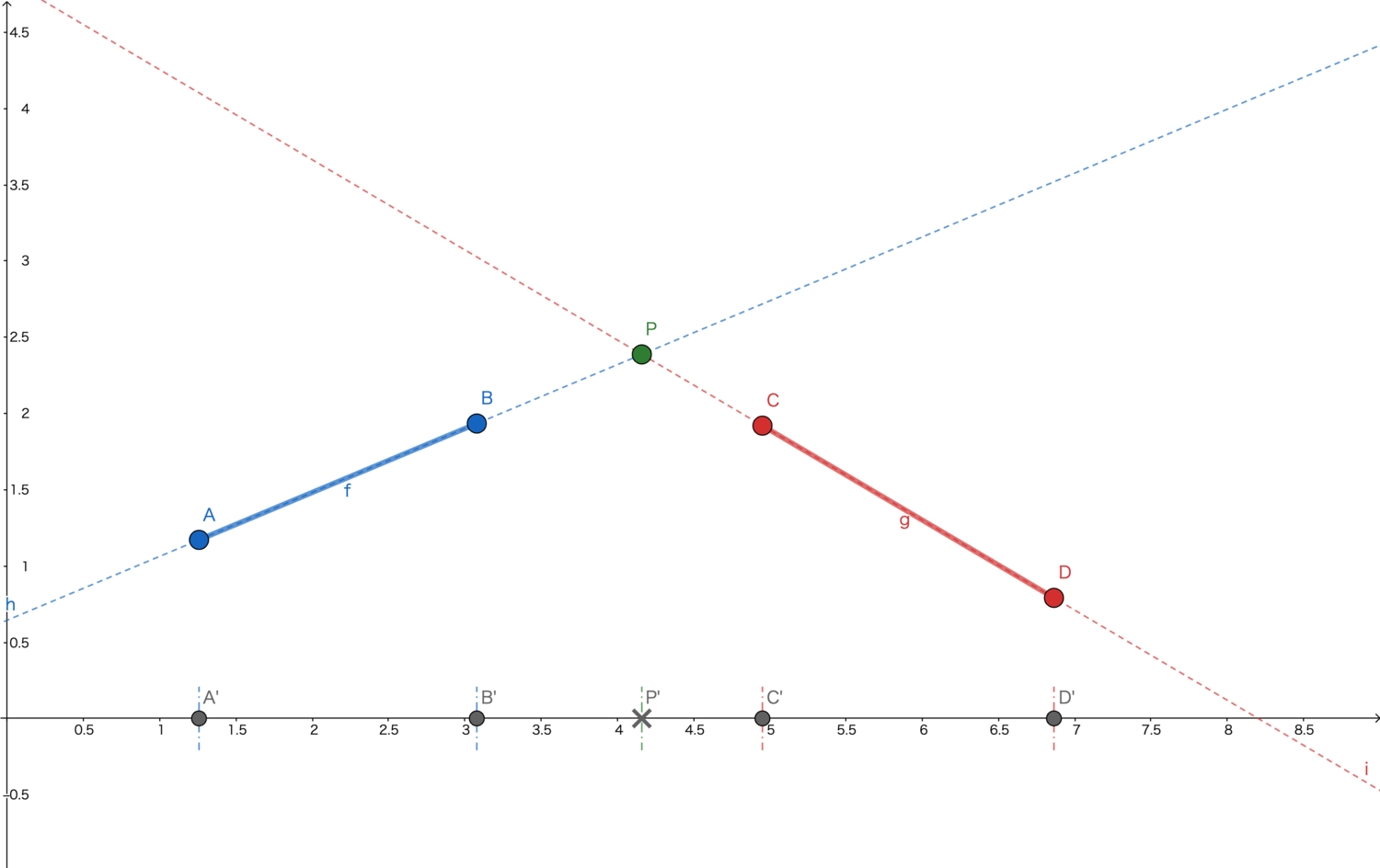
下图的线段g与线段f所在直线h的交点为P，但是线段f和线段g也不相交。

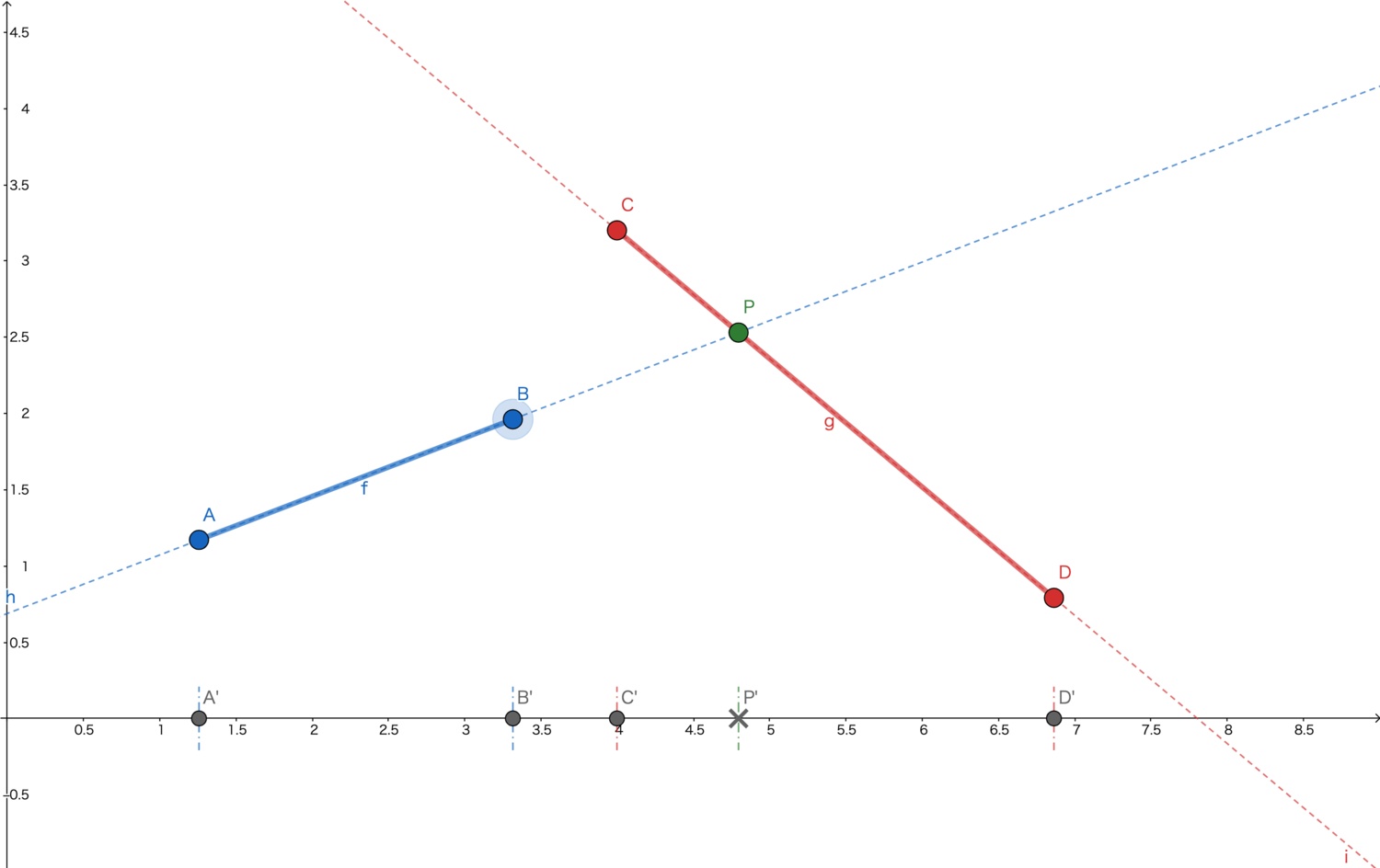
下图当中的线段g与线段f相交，交点为P。

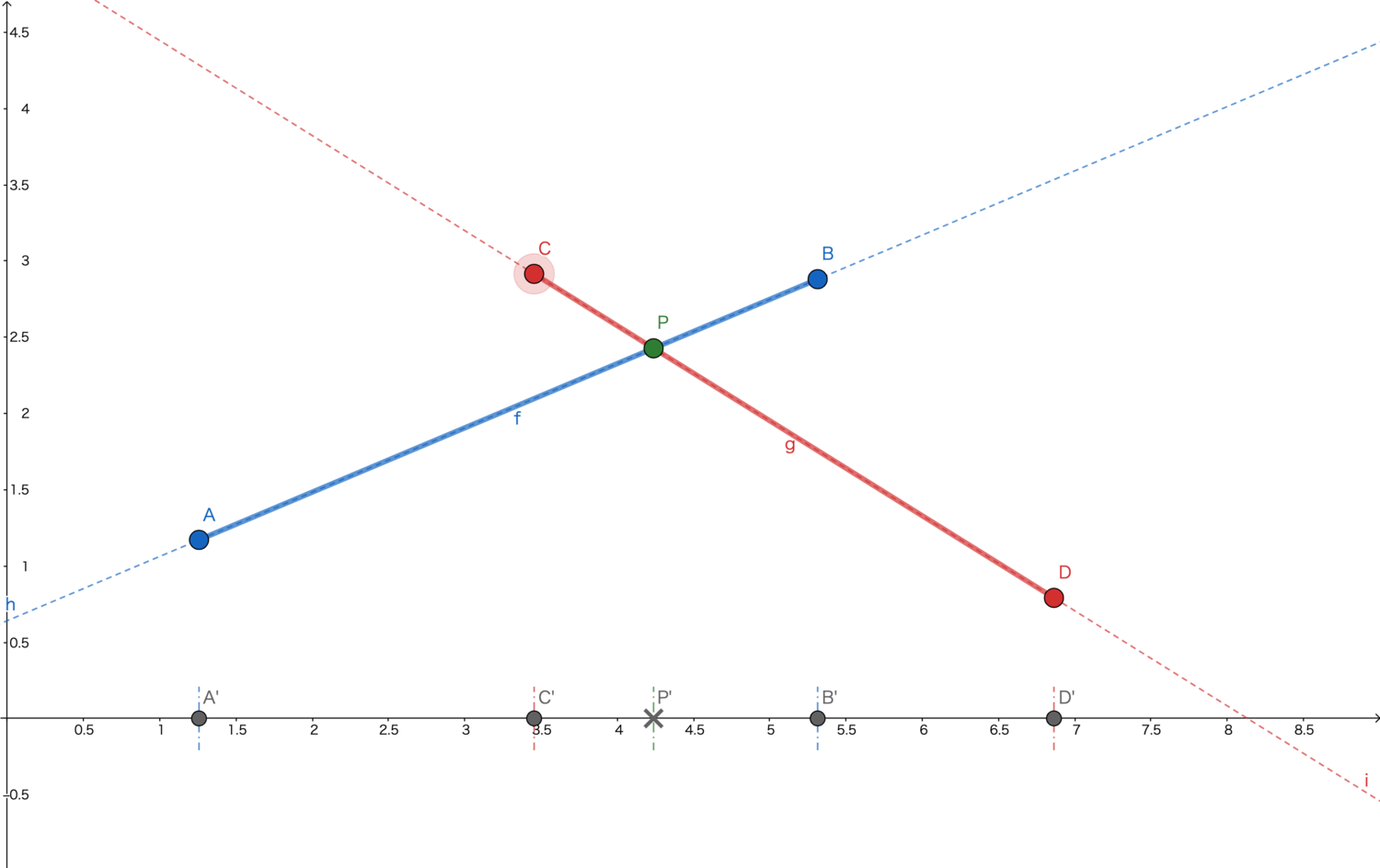
观察图片可以发现只有交点P的x坐标同时位于线段f的端点A与B、以及线段g的端点C和D的x坐标之间的时候，点P才是线段的交点。
通过比较交点位置向量的x坐标和两条线段端点的x坐标（ray.begin.x、ray.end.x）可以判断。

可以通过GeoGebra修改线段位置和长短来查看效果。

将上述逻辑通过intersection(Ray)方法实现：

class Vector{
  number x,
  number y
}

class Ray{
  Vector pos,
  Vector way

  get begin(){}
  get end(){}

  Vec intersection(Ray)
}

至此第二个问题也得以解决。

从解决上面两个问题的过程中，可以总结出关于代码复用的两个结论。

成员变量中心化

定义成员变量的时候，要考虑从这个成员变量到达各个派生出来的属性或者特定值的“最远距离”是不是比较均匀。
比如定义Ray类的时候，如果选用两个端点作为成员变量的时候，或许在位置计算上比较方便，但是在方向方面的运算比较复杂。
如果运用场景中恰恰又是方向运算多的话，就显得不灵活了。

中心化往往伴随着直观化。回想在纸上画线段的样子，是不是也是从一个点起笔，沿着某个方向画下去？
或许数学上的定义突出两个端点的重要性，但是位置与方向是线段两个最直观的属性，两者兼顾的成员变量可以让类的方法实现显得更灵活，无论是成员变量还是方法，复用性都会得到提升。

繁琐逻辑黑盒化

上述求线段交点的问题中，谁都没法否认这是很简单的数学问题，但是同样谁也没法否认需要拿笔算算、拿纸画画才能得出结果。
这种数学原理简单但是运算繁琐的逻辑，如果每次都要重新考虑实现的话，会造成思维上、心理上的压力。
而且，还有随之而来的临界值问题，如果线段与坐标轴平行怎么办？两条线段平行的话怎么办？数值过大导致越界怎么办？
如果不是每次都能做到完整的临界值分析的话很容易出现错误。
将相同的逻辑集中在一个地方管理，那么再遇到类似问题不需要考虑内部逻辑直接使用即可，即使出错了集中对应以后也可以一劳永逸。

综上，个人认为能够达到上述要求的代码适合实施代码复用。

3.代码实现与文档生成

在完善一些基本运算函数的基础之上，按照上述思路用JavaScript实现逻辑。

源代码：https://github.com/7mA/linear-algebra-js-lib/blob/master/src/linear-algebra-lib.js

虽然在实现之前就能把所有函数都能考虑到并且设计出来是理想状态，但是往往不太可能。
比如Vec类的move()方法就是在实际使用过以后才追加的。

/**
 * 移动向量
 * @param {number} distance 移动距离
 * @param {number} angle 移动角度
 * @return {Vec} 移动以后的向量
 */
 move(distance, angle){
   return this.add(new Vec(cos(angle), sin(angle)).multi(distance));
 }

可以看到move()方法用到了已经定义好的add()和multi()方法。
追加的方法用到已经定义好的方法并不是冗余，相反正是复用性的体现。
的确沿某一个方向移动一定距离就可以看作是与该方向的单位向量与距离的积求和的过程。
但是在给定角度与距离之后，每一次都需要这样一次思考，显然是无意义的反复。
所以这里追加一个方法就可以省掉这样一步变换。

另外关于是否需要更加细化，比如加一个moveToLeft()的方法表示向左移动的问题，我个人的看法是，行为是方法化的对象，怎样做行为应该交由参数来决定。这是为了增加方法的通用性，同时也是最大化复用性的做法。

既然是用于复用的代码，清晰易懂的注释是必不可少的，同时还可以通过规范化的注释块来生成API的说明文档。

首先类的注释块中需要说明类的逻辑定义和成员变量（properties）：

/**
 * 向量类
 * @prop {number} x 向量横坐标
 * @prop {number} y 向量纵坐标
 */

方法（methods）的注释块中除了函数说明以外，还需要说明参数和返回值的型与逻辑定义：

/**
 * 计算两个向量的和
 * @param {Vec} b 向量和运算对象
 * @return {Vec} 向量的和
 */

存取器（accessors）的注释块与方法的有区别，指定的不是返回值而是型：

/**
 * 线段起点的位置向量
 * @type {Vec}
 * @readonly
 */

因为Ray类里的起点和终点位置变量只设置了取值器（getter），所以注释中增加了@Readonly注解。

在填写完足够的注释以后，可以用JSDoc生成API说明文档。

1	npm install -g jsdoc

到项目根目录里使用下列命令生成文档：

1	jsdoc ./src README.md -c ./conf.json

其中./src和README.md为生成文档的对象，JSDoc会到./src目录下寻找所有的js文件并且生成html格式的文档，并且将README.md内的内容显示在首页。
-c选项为指定配置文件，以下是配置文件的内容举例：

{
  "opts": {
    "template": "node_modules/tui-jsdoc-template",
    "destination": "./docs/"
  },
  "templates": {
    "name": "liner-algebra-js-lib API Docs"
  }
}

其中opts.template可以设置生成页面使用的模版，opts.destination可以指定生成的页面文件的目录。默认值为./out/。
templates选项下可以设置模版内的相关内容，比如templates.name设置的是页面的共通标题。

生成效果可以参考liner-algebra-js-lib API Docs。

4.发布npm包

如此一来，本地已经有了源代码和说明文档。为了能够更加方便地运用，放到云端是一个好的措施。
当然甩到github上，用的时候再复制粘贴好像也能用，毕竟刚开始行数又不多。
但是在一些云端的开发环境或者在线的编辑器当中，并没有充足的地方来多塞上额外的JS代码，所以果然最理想的状态还是能远程调用。
利用npm将库打包发布以后，就可以使用CDN远程访问了。

打包之前首先要把项目目录初始化成一个npm项目。

npm init

name: (linear-algebra-js-lib)
version: (1.0.0)
description:
entry point: (index.js)
test command:
git repository:
keywords:
author:
license: (ISC) MIT

按照实际情况填写各字段，括号内为默认值。

之后需要到npm官网注册账号。
注册完毕以后，就可以在本地登陆了：

npm adduser    

Username:
Password:
Email:

最后可以用npm who am i来确认一下登陆状态，登陆成功就可以开始发布操作了。

在打包发布之前需要定义一下.npmignore文件。与.gitignore文件类似，其中定义了项目目录下不会被打包上传的内容。

1
2
3

/**/*
!src/linear-algebra-lib.js
!ACKNOWLEDGEMENT

上述配置意味着除了src/linear-algebra-lib.js以外的内容都不会被打包上传。

使用下列命令打包发布：

1	npm publish

之后可以到npm的个人主页上查看自己的包是否发布成功，或者干脆直接用安装命令试试能不能安装也可以。

1	npm i linear-algebra-js-lib

在npm的package.json中有一个version字段，表示提交时包的版本。
npm在版本控制上比较严格，要求提交的版本必须比已发布的版本高。
所以需要手动更改package.json的version字段，或者使用npm version <update_type>命令。

npm的版本格式为x.y.z，被成为“语义化版本（Semantic versioning）”。
版本的更新应符合以下规则：

修复bug或者小改动，增加z，如1.0.0 -> 1.0.1
增加新特性，但是可以向后兼容，增加y，如1.0.1 -> 1.1.0
有较大改动，无法向后兼容，增加x，如1.1.1 -> 2.0.0

可以用npm version <update_type>命令按照上述规则自动更改版本。
<update_type>可以为patch、minor、major，分别对应上述三条规则。

成功发布以后，就可以到jsdelivr搜索查看自己的包，用CDN链接访问JS文件了。

1	https://cdn.jsdelivr.net/npm/linear-algebra-js-lib@1.1.8/src/linear-algebra-lib.min.js

5.远程使用

发布成功以后，就可以不受开发环境限制地远程使用自己的包了。

下面是在CodePen的在线开发环境中使用linear-algebra-js-lib的示例。
鼠标拖拽可以移动十字中心点的位置，左右方向键可以旋转十字的角度，黄色的点代表蓝色十字与黑色井字的交点。
通过左下角的Resources按钮可以看到远程调用的JS文件。

See the Pen p5js-linear-algebra-lib by Kaku (@7ma) on CodePen.

从上面的示例可以看到，只要知道角度和距离，通过十字中心点来确定四个方向的端点只需要一个move()函数就可以解决，不需要关心到底是怎么计算的：

let vpBeamList = [];
for(let i = 0 ; i < 4; i++){
  vpBeamList.push(
    Ray.getRayFromPoints(
      vp.pos,
      vp.pos.move(75, vp.angle + i * PI / 2)
    )
  )
}

绘制交点也不需要实现复杂的运算过程就可以简单完成：

for(let hl of horizontalLineList){
  let crossPosVec = vpBeam.intersection(hl);
  if(crossPosVec){
    point(crossPosVec.x, crossPosVec.y);
  }
}

6.总结

说到最后代码复用其实也不是什么华丽的技巧，甚至还略显朴素。
但是程序的设计就是一点点累积的，小处井井有条，才有能变大的那一天。
注重代码复用，才能让既存代码积累成日后的经验加成，而不是运用和维护的债务。
毕竟不是什么程序都可以像hackthon的作品那样做完就扔的。

Reference Source:

JavaScript代码复用实践：从类定义到npm发布

Contents