matplotlib实现算法可视化

1.关于matplotlib

matplotlib是一个Python语言的2D绘图库。
它支持各种平台，并且功能强大，能够轻易绘制出各种专业的图像，例如：直方图，波谱图，条形图，散点图等。并且，可以非常轻松地实现定制。

---

2.获取matplotlib

关于如何获取matplotlib，官网有一个专门的介绍页面。
最直接的方法是通过pip安装：

sudo pip3 install matplotlib

在Python中使用matplotlib，按照需求引用对象（matplotlib.*）或者特定函数（from matplotlib.* import *）即可。

# 引用对象
import matplotlib.pyplot as plt

# 引用函数
from matplotlib.patches import Rectangle

---

3.基础用法示例

matplotlib最广泛的用途就是在坐标系中绘制各种各样的图。
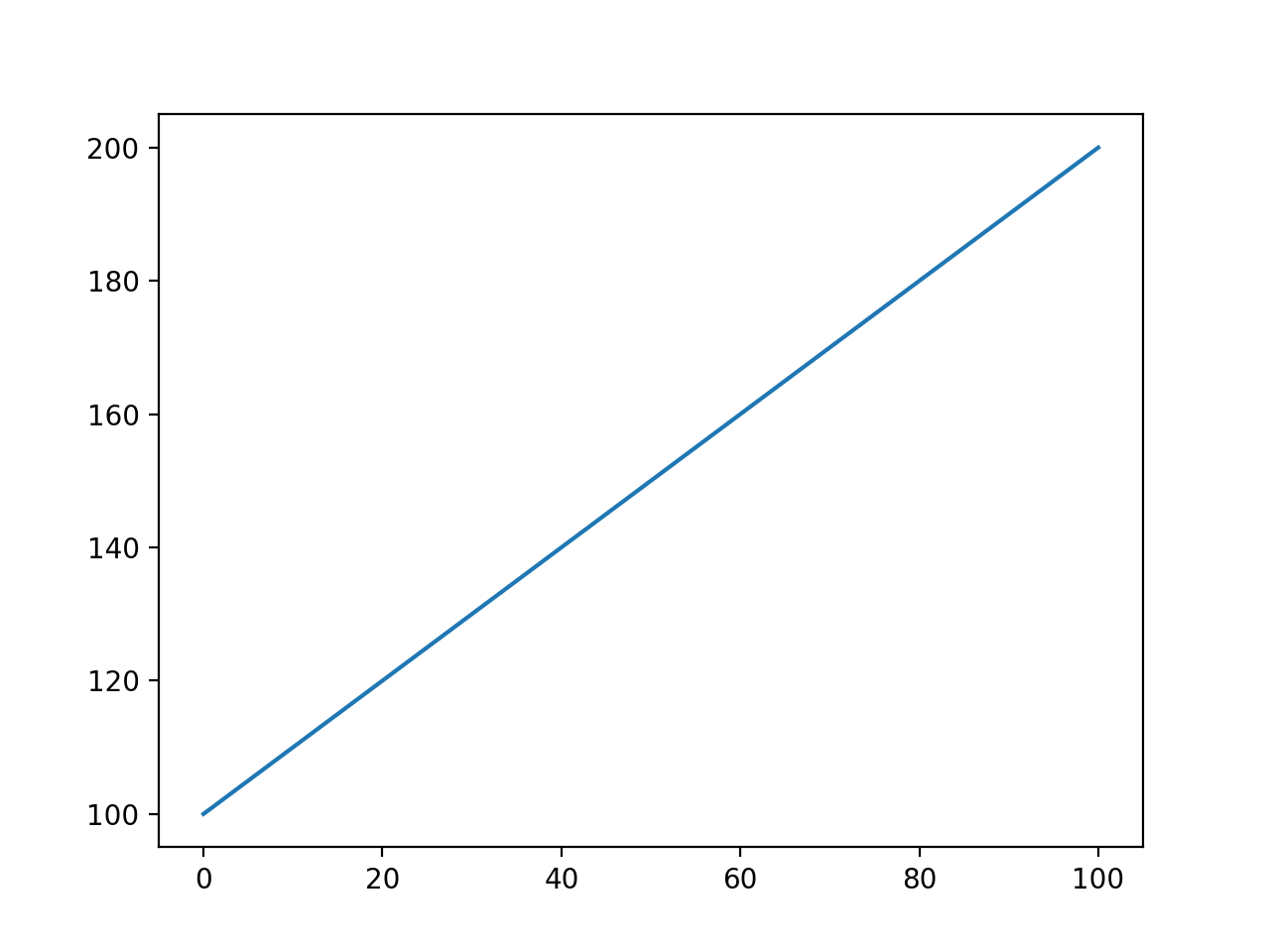
比如下面的代码就可以绘制出一副简单的线性图：

import matplotlib.pyplot as plt
import numpy as np

data = np.arange(100, 201)
plt.plot(data) # 将数据映射到坐标系中
plt.show() # 绘制图像

---

4.算法可视化：以广度优先搜索为例

既然matplotlib可以将运算逻辑中的数据可视化成直观的图像，那么算法的运算过程也同样可以用合理的图直观地表现出来。

下面以广度优先搜索解决方格棋盘最短路径长度问题为例，将算法的运算过程可视化。

源代码：https://github.com/7mA/bfs-shortest-path-binary-matrix/blob/master/bfs.py

4.1 问题分析

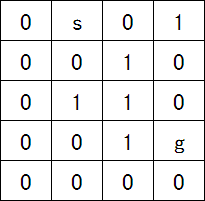
算法的场景是一个方格棋盘，可以看作坐标系上的一个二维矩阵，不同属性的方格用不同的样式表示出来。

算法的过程是从起点通过广度优先搜索的方式求到达终点的最短距离。
每增加一次搜索距离，都将有若干个方格的距离得以确定。
因此，可以在确定一个方格或者增加一次距离的同时，绘制出当前的确认情况，通过这种方法来获知算法的运算过程。
为了直观地表现，不同距离的方格可以用不同方式表示出来。

4.2 代码实现

首先在算法的最开始，定义过程图的基本信息：

# 调整过程图的大小
plt.figure(figsize=(5, 5)) # 500px * 500px

ax = plt.gca()             # 获取坐标系对象
ax.set_xlim([0, w])        # 将矩阵宽度设置为x轴最大值
ax.set_ylim([0, h])        # 将矩阵高度设置为y轴最大值

之后，在根据输入来初始化棋盘的数据结构的同时，将棋盘上各方格的信息也投射到过程图的坐标系中。
投射的时候要注意二维数组的下标与坐标系里的坐标之间的映射关系。

# 定义方格样式与位置
rec = Rectangle((j, h - i), width=1, height=1, facecolor='b', edgecolor="gray")
# 将起点方格加到坐标系中
ax.add_patch(rec)

初始化结束以后，对图像布局进行调整。

# 设置图像的坐标轴比例相等并且隐藏坐标轴
plt.axis('equal')
plt.axis('off')
# 压缩图像边距
plt.tight_layout()

之后，在算法逻辑执行的过程中，为了确认算法的运算过程，需要在状态更新的同时更新坐标系中的内容。
在广度优先搜索中，算法每更新一个方格的距离信息，坐标系中对应的方格就需要进行更新，同时还可以根据需要保存快照。

# 方格填充步数
plt.text(nx + 0.5, h - ny + 0.5, step,
  fontsize=7.5, verticalalignment="center", horizontalalignment="center")
# 单步保存过程图
saveImage(plt)

# 保存图片函数
def saveImage(p):
    millis = int(round(time.time() * 1000))
    # 需要提前准备好/img目录，以毫秒数命名
    filename = './img/' + str(millis) + '.png'
    p.savefig(filename)

这里将距离信息直接以文本的形式写到对应方格当中。

经过反复的运算以后，终点的距离信息得到确定。在最后输出结果的时候，可以保存最终的结果图像，以备参考。

# 调整y值以调节结果文本位置
plt.title("%s steps" % step, fontsize='15', fontweight='bold', y=-0.03)
# 保存结果图像
saveImage(plt)

将上述绘图代码如影随形地插入到算法当中，每执行一次算法，就可以输出当次执行的运算过程。

4.3 运行结果

下面以输入为5*5的棋盘的情况为例。

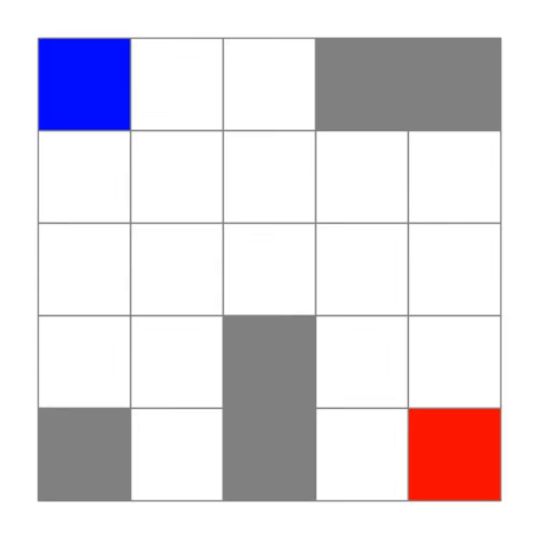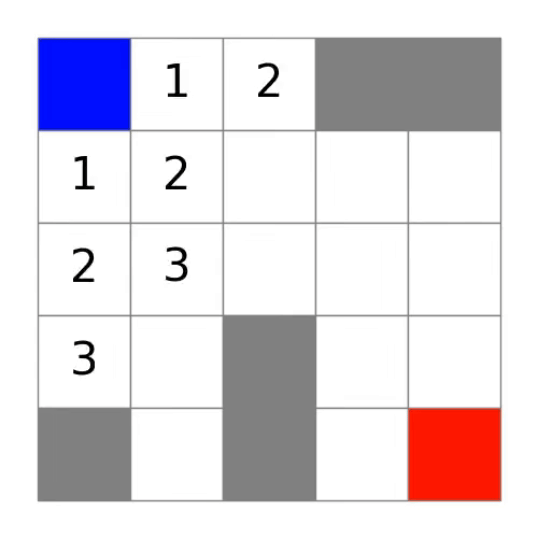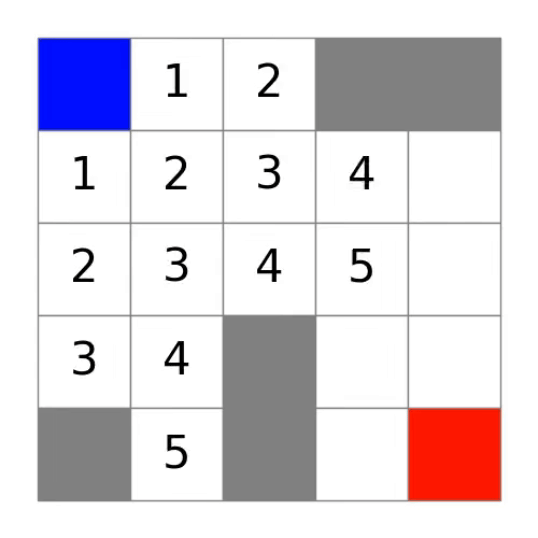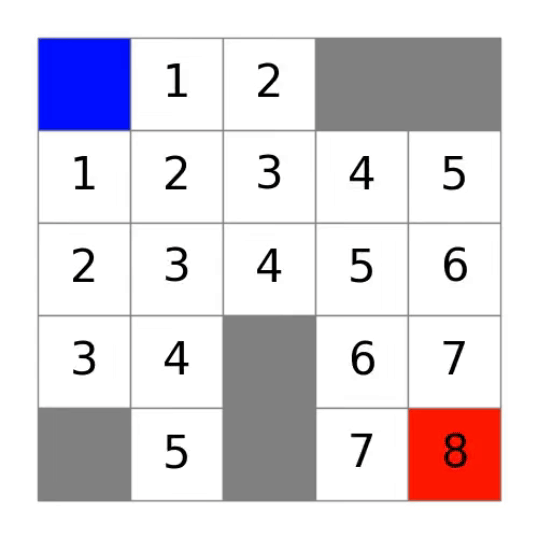
棋盘初始化：

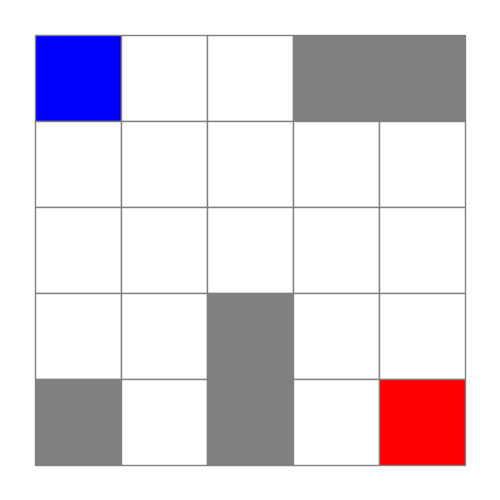
其中左上角的蓝色代表起点，右下角的红色代表终点，灰色代表墙壁，白色代表道路。

算法搜索完距离为1的方格以后：

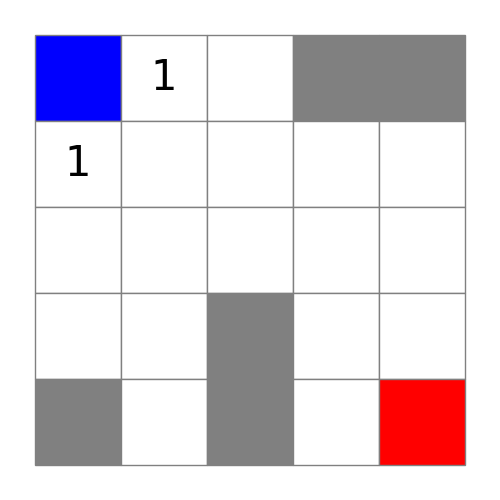
距离为1的方格内添加了文字表示距离。

算法搜索完距离为2的方格以后：

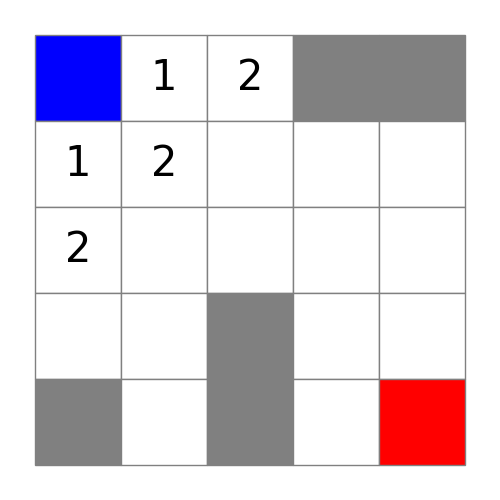
同样，距离为2的方格也表示在图像当中。

继续执行算法：

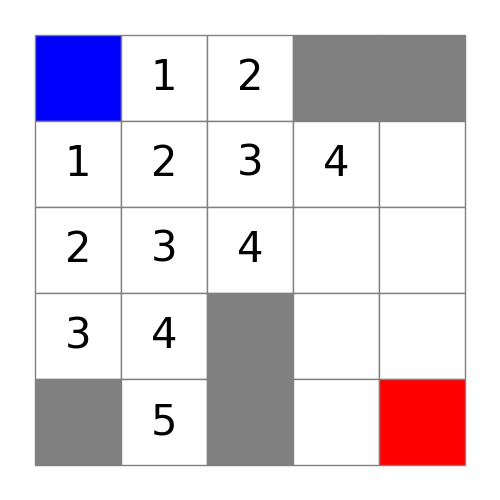
最后得到结果图，可以看到起点到终点的最短距离为8:

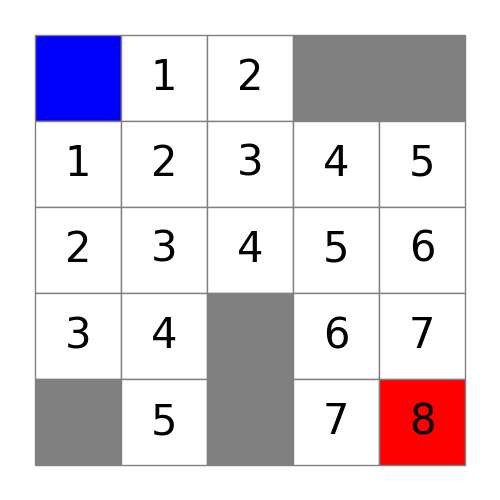
为了更加直观地表现出算法运算的过程，可以把过程图合成为动图。
合成动图可以使用ImageMagick。

brew install ImageMagick

通过下列命令可以将当前目录下所有png格式的图片合成为名为animated.gif的动图文件，-delay用于控制每张图片的停留时间。

convert -delay 50 *.png animated.gif

将算法运行得到的所有过程截图合成为动图如下所示：

通过相同方式，还可以得到10*10棋盘的算法执行过程与结果。

10*10棋盘初始状态如下，起点与终点仍分别位于左上角和右下角：

10*10棋盘的运行过程：

10*10棋盘的运行结果：

类似地，20*20棋盘的执行过程与结果如下：

可以看到，20*20的情况下，数字已经略显密集了。再增加棋盘大小的话，图像的直观性势必要下降。
所以，针对规模再大一些的数据，需要对可视化方法进行一点调整。

4.4 视觉优化

对于更大规模的数据，可以使用比数字更加直观的颜色来表示距离，不同的颜色表示不同的距离。

之前的图中使用蓝色作为起点的颜色，使用红色作为终点的颜色。
那么可以考虑用蓝色与红色之间的渐变色来表示与起点与终点之间的距离关系。
越接近蓝色代表距离起点越近，越接近红色代表距离终点越近。

# 方格填充渐变色
rec = Rectangle((nx, h - ny), 1, 1, color=colorGradient(step, h, w))
ax.add_patch(rec)

def colorGradient(current_step, height, width):
    # 根据高度和宽度调整适用于颜色渐变的最大步数
    gradient_step_threshold = (height + width) * 1.1

    color_start = [0, 0, 1.0]  # color: b(blue)
    color_goal = [1.0, 0, 0]  # color: r(red)
    if step < gradient_step_threshold:
        return [(color_goal[0] - color_start[0]) * current_step / gradient_step_threshold, 0,
                color_start[2] + (color_goal[2] - color_start[2]) * current_step / gradient_step_threshold]
    else:
        return color_goal

需要注意的是，广度优先搜索中其实每一次只更新与起点的最短距离，与终点的最短距离是无从得知的。
所以这里要设置一个gradient_step_threshold作为预想的渐变极限值，理想效果为当与起点的距离达到这个极限值的时候刚好到达终点。

当然是不可能事先知道这个最佳的渐变极限值是多少，所以这个值只能大概接近于预想的起点到终点的最短距离。
如果实际的最短距离大于渐变极限值，那么距离超过渐变极限值的方格的颜色一律与终点相同。
如果实际的最短距离大于渐变极限值，那么终点前一个方格的颜色会与终点的颜色有一个较大的差别。
不过上述视觉上的影响在相对准确的预估和大规模数据下可以忽略。

同时由于数据规模较大，不需要每更新一个方格就保存一次图像，所以可以通过更改保存时机和保存步长来调整过程图的差分。

# 整合保存过程图，通过求余除数调整步长
if step % 2 == 0:
    saveImage(plt)

在做了如上调整以后，对50*50的棋盘运行算法。

为了观察渐变色的效果，先在空棋盘上尝试。

其运行过程如下：

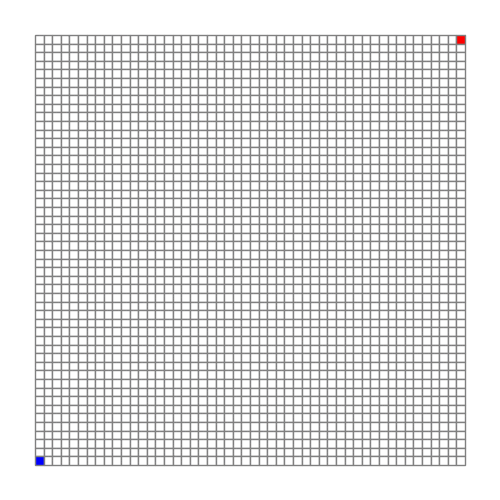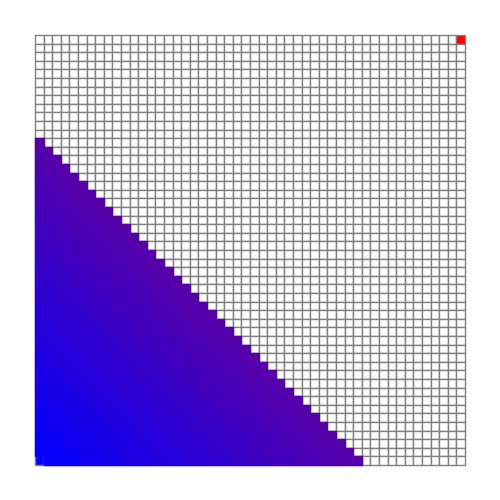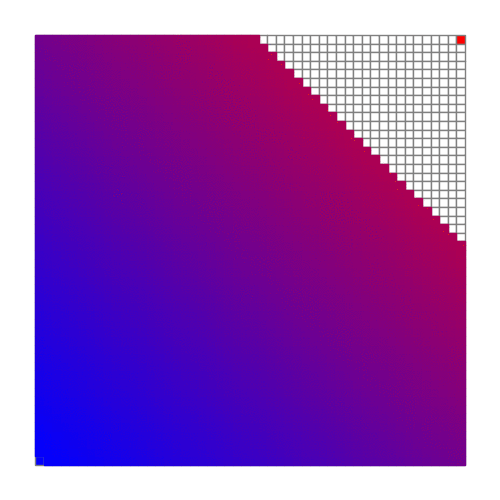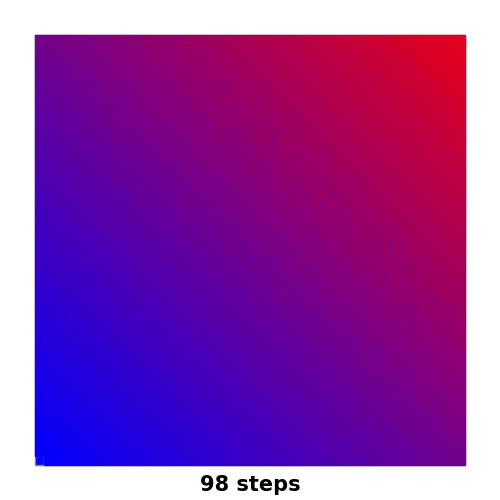
可以看到，结果最后成为了一张“光滑”的渐变色图。
这也符合广度优先搜索在没有墙壁的棋盘上的执行结果。

下面在随机生成的50*50棋盘上执行。起点位于左下角，终点位于右上角。

运行过程如下：

整个过程类似于洪水漫灌的效果，不同的颜色代表洪水到达时机（与起点的最短距离）的不同。
可以看到因为墙壁的影响，颜色的渐变出现了不均匀的现象。
但是也正是不同的渐变色直观地表现出方格与起点之间的距离关系。

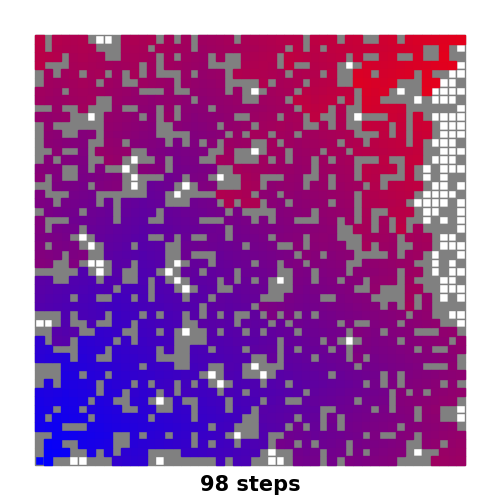
当然，也并不是所有的棋盘都能满足起点与终点连通的。
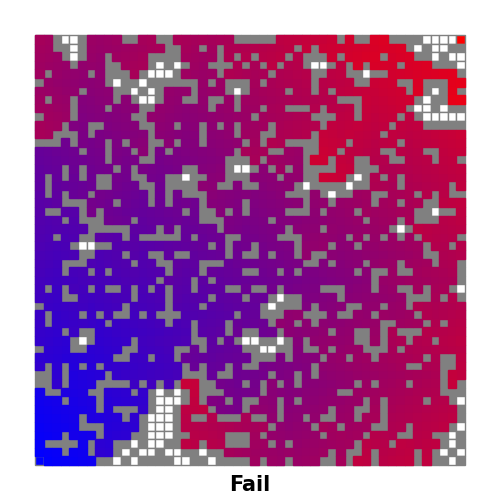
下面这个就是结果为Fail的例子。

结果图像中终点与其他未填色的方格都是不与起点连通的方格。

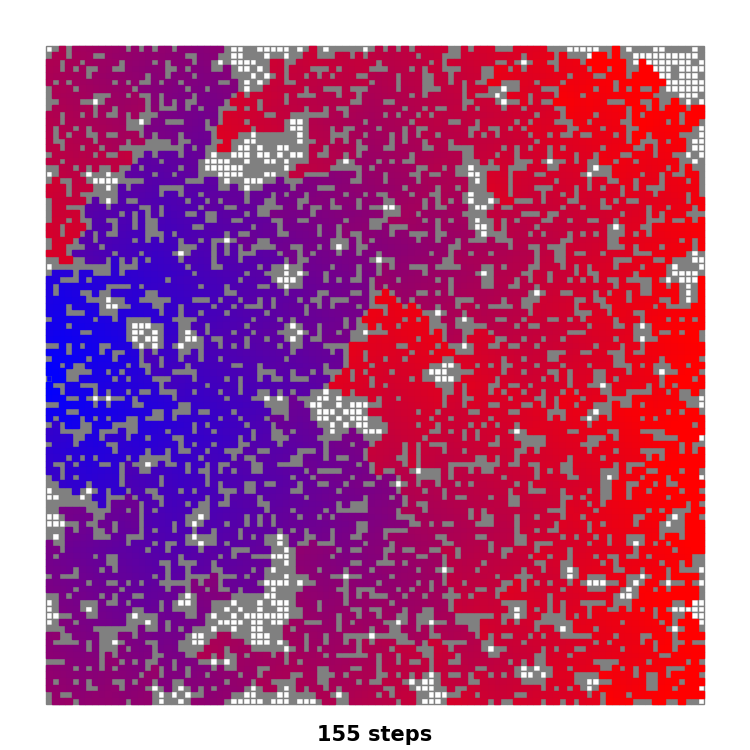
100*100棋盘的效果如下，起点位于左侧边缘的中点，终点位于右侧边缘的中点。

由于数据规模增大，渐变色与距离的差分比例更小，所以渐变色也会更细腻一些。

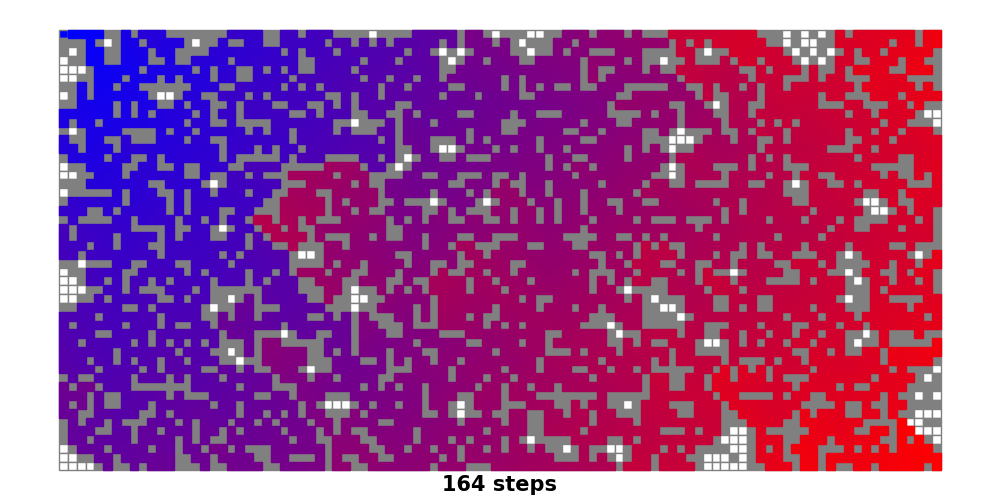
当然，宽与高不相等的矩形棋盘也可以适用。下图为100*50的棋盘，起点与中点分别位于左上角与右下角。

不难发现，如果在没有墙壁的情况下，左上角到右下角的最短距离应为height + width - 2，即一直采取向右或者向下的移动行为。
因为墙壁的存在，有可能不得不采取向左或者向上的移动策略来形成最短路径，所以距离也有可能随之增加。

4.5 大规模数据

下面对大规模数据进行尝试。棋盘大小为1,000*1,000，共有1,000,000个方格。

使用matplotlib生成初始化图像：

起点和终点的蓝色与红色早已被淹没在白色和灰色的像素点之间了。
这里说明一下，以左上角定点为原点，右方向为x轴正方向，下方向为y轴正方向的话，起点位于(100, 100)，终点位于(900, 900)。
如果把图片放大，就可以找到微小的蓝色与红色像素点。

放大10倍以后的终点：

需要注意的是，棋盘大小已经达到1,000*1,000，需要留意单个方格与像素点的关系。
前文的例子中所有的方格均有灰色边框，由于边框本身就占据像素点，所以开启边框的话，结果很可能就被边框占满像素点，图像变成一片灰色。
因此在生成1,000*1,000棋盘的图片的时候，我提前把方格边框关掉了。
由于需要将1,000,000个方格的信息一个不漏地反映到坐标系中，而且还要以像素为单位地绘制一张分辨率为1,000*1,000以上的图片，matplotlib在生成这张图片的时候就消耗了数分钟的时间。

由于绘制图像本身的时间成本太高，所以运行算法的过程只截取了确定距离为1,000的方格之后的图像。

感觉还蛮像花瓣或者墨水滴在纸上的样子，或者星空。
通过高粒度的差分才能生成如此自然的渐变色，不得不再次感叹自然界的神奇。

算法的最终结果如下：

方格的颜色从左上到右下以蓝、靛、紫、品红、红的顺序依次渐变，最后停留在右下角的终点处。
夹杂着的白色方格为被墙壁隔开的不可达区域。
最终计算出起点到终点的最短距离为1,644。
本来在2秒之内就可以运行完毕的算法，由于绘图逻辑的存在，运行时间超过了一个小时。

program complete: 4146 seconds

再次为结果图像的艺术性惊奇的我一时兴起按照专辑封面的风格对其加工了一下：

5.总结

利用matplotlib进行算法可视化的基本思路与插入log输出的思路类似，无非就是将算法过程中的状态以图片的方式留存下来。
这次的例子中是实时保存截图的方式来获取随时间变化的过程，此外还可以将时间作为图像坐标系的维度之一，将不同时间下的状态反映在同一个坐标系中。
因为matplotlib本身也支持3D绘图，所以在需要三维空间表示三维数组的数据演变过程的时候，这种思路同样适用。
另外，在获取最短路径的路线这种直到算法最后才知道正确结果的问题中，也可以在算法结束后自定义截图的保存方式，以获得更好的可视化效果。
像下面这个例子，在算法运算结束以后路径列表已经全部获取到了，但是为了表现出沿着路径到达终点的动态效果，在最后的绘图逻辑中仍然以遍历路径列表的方式按照单次移动为单位保存截图。

def BuildPath(self, p, ax, plt, start_time):
    path = []
    while True:
        path.insert(0, p) # Insert first
        if self.IsStartPoint(p):
            break
        else:
            p = p.parent
    for p in path:
        rec = Rectangle((p.x, p.y), 1, 1, color='g')
        ax.add_patch(rec)
        plt.draw()
        self.SaveImage(plt)

---

Reference Source:

1. Python绘图库Matplotlib入门教程
2. 路径规划之 A* 算法